Lecture 5 - Michael Thomas

---

Activation Functions and XOR Networks

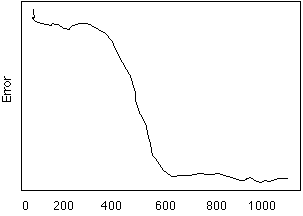
The following is the LMS Error plot of one learning session for the XOR Network. From this a number of question arise.

Questions

• Why the sudden initial drop?
• Why the long plateau?
• Why the sudden long drop?
• Why the final plateau?

Explanations

First, we plot the hidden unit space, just like we had plotted the input space.

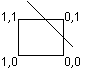
How? y=ax+b PLug in patterns get...

Epoch 0	Ep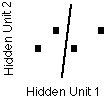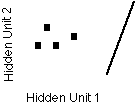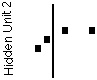och 100
Epoch 200	Epoch 300 Hidden Unit 1

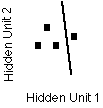
Notice, the network changes the hidden to output weights more than the input to the hidden weights. This is because the input to output weights are a derivative times the derivation. In essence the error is diluted every step back.

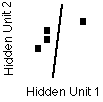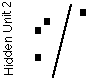Epoch 300	Epoch 400 Hidden Unit 1
Epoch 450	Epoch 2000

Notice again, that the network hasn't completely reach the global minimum, rather the point corresponding to 0,0 is still in the lower left. Clearly, it should be more right, for everything to be hunky dorry, BUT the network won't do this as it already spent too much time strengthening the weight in the wrong direction.

How is this changing the activation function?

Well, of course, the sigmoid function never acctually changes, BUT the connectivity of the network can change the part of the sigmoid function each individual unit uses. For Michael's money, if the output units responds differently to different inputs (aka, moving from a linear to a sigmoid), then this is effectively changing the activation function.
     Indeed, the output unit of the XOR does change its responding, from linear, to sigmoid, to linear and back again. Why? Because as the net input changes, the slope of the sigmoid function changes. Thus, the larger the net input, the steeper the sigmoid slope.