Lecture 3: Terms to Know

---

Perceptron Convergence Rule - Learning rule which uses the error at output to adjust weight and threshold changes accordingly. While less "complex" than some other rules, it nonetheless "guarantees" to find a solution, if such a solution exists. Part of the class of Gradient Descent Algorithms.

Gradient Descent Algorithms - Means of learning which calculates the "slope" of the error curve (Error Signal) at any particular state and then attempts to move down that slope. Hence, it "descends down the error gradient." Widrow-Hoff 1960 proposed one of the first versions of this, the Least Means Square Error.

Least Means Square Error - The error between target and output, squared. One means of calculating and error signal.

Error Signal - The change in error as a function of the change in weight. Or in Calc, d(error)/d(weight). OR d(T-W*Ain)squared/dw OR a constant times the error times the activation at input. Well, wouldn't it be nice to know the entire slope of the error and just find the bottom? Well, yes, but A) that requires a lot of computational power, and B) most models assume that the nework only has local information available when making changes (much like hiking down a mountain at night: even if can't see the bottom, you know that if you keep going down, you'll get there.)

Note: Although this guarantees you wil find the Global Error Minimum, who is to say that this minimum is zero? Acctually, in fact, Minsky and Papert say it definately won't be zero, unless the input patterns are Linearly Independent.

Linear Independence - When the input patterns are independent. That is, they have absolutely nothing in common. Thus, for example, one can think of the Boolean AND & OR as Linearly Independent. Solving them, thus involves partitioning the Problem Space.

Linearly Separable - Refers to a problem space which can be partitioned in such a manner as to seperate the sets you want via a line (or plane, or hyper plane, depending on the dimensionality).

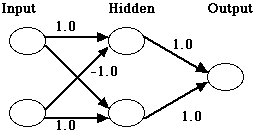
XOR Problem - Classic connectionist problem which turns out not to be linearly separable. At least given the classic input structure and activation functions (AN: What about an activation function which is a normal curve?), and no hidden units. If instead, we use hidden units, than the following network will solve the problem nicely.

How? The hidden units are effectivly "re-representing" the input patterns (warping the input space, if you will). In this manner, the problem has the capacity to "overcome the tyrrany of similiarity" and transform a problem space which is initially inseparable into one which is now linearly seperable.

BackPropagation - Type of gradient descent algorithm which finds a way to assign blame to the hidden units, by effectively turning the network on its head and "backpropagating" the error throughout the network and therby assigning the appropriate amount of blame to each of the responsible hidden units. This mechanism is extroardinarily powerful

Note: Backpropagation only works for activation functions with a definable slope at every point on their curve. Eg. logistic or linear, but not linear threshold. Although, since even linear threshold can be aproximated by a continous curve, backpropagation can effectively solve any problem.

WARNING: Although backpropagation guarantees that a solution exists, it doesn't guarantee it will find it. Thus, should, it find a bump in the weight space, it can get caught in a local minimum, and will not learn. Still there are various tricks, to avoid such, none work perfectly (changing the learning rate, momentum, or temperature).